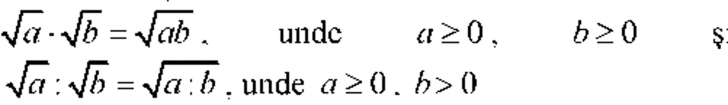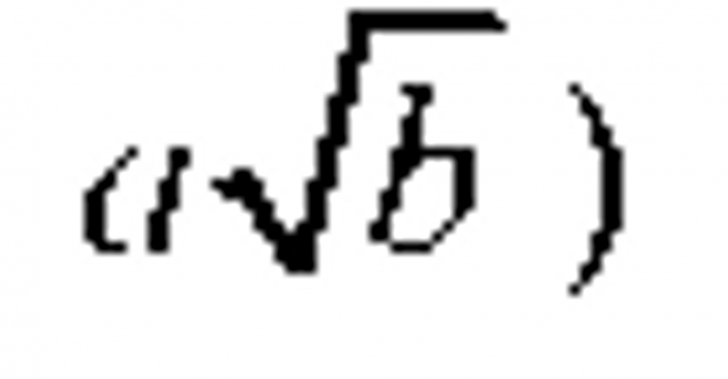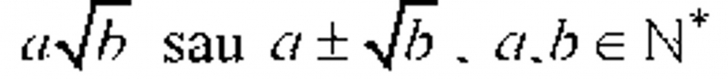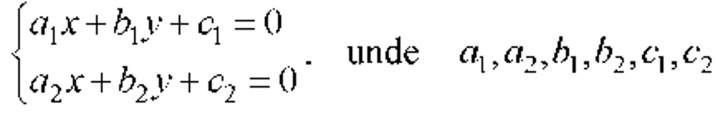Anexa nr. 1 - CALENDARUL DE DESFĂȘURARE A. - Ordinul MEN nr. 4431/2014 - organizarea şi desfăşurarea evaluării naţionale pentru absolvenţii clasei a VIII-a în anul şcolar 2014–2015
| Index |
|---|
| Ordinul MEN nr. 4431/2014 - organizarea şi desfăşurarea evaluării naţionale pentru absolvenţii clasei a VIII-a în anul şcolar 2014–2015 |
| Anexa nr. 1 - CALENDARUL DE DESFĂȘURARE A. |
CALENDARUL DE DESFĂȘURARE A
EVALUĂRII NAȚIONALE PENTRU ABSOLVENȚII
CLASEI A VIII-A
ÎN ANUL ȘCOLAR 2014-2015
13 iunie 2015 | Încheierea cursurilor pentru clasa a VIII-a |
15-17 iunie 2015 | Înscrierea la Evaluarea Națională |
22 iunie 2015 | Limba și literatura română - probă scrisă |
23 iunie 2015 | Limba și literatura maternă - probă scrisă |
24 iunie 2015 | Matematica - probă scrisă |
26 iunie 2015 | Afișarea rezultatelor (până la ora 16) |
26 iunie 2015 | Depunerea contestațiilor (orele 16 - 20) |
27 - 29 iunie 2015 | Rezolvarea contestațiilor |
30 iunie 2015 | Afișarea rezultatelor finale după contestații |

PROGRAMA
PENTRU DISCIPLINA
LIMBA ȘI LITERATURA ROMÂNĂ
EVALUARE NAȚIONALĂ 2015
PROGRAMA DE EXAMEN PENTRU DISCIPLINA LIMBA ȘI LITERATURA ROMÂNĂ
I. STATUTUL DISCIPLINEI
Limba și literatura română are, în cadrul evaluării naționale de la finalul clasei a VIII-a, statut de disciplină obligatorie.
Prezenta programă pentru evaluarea națională de la finalul clasei a VIII-a la disciplina limba și literatura română vizează evaluarea competențelor elevilor de receptare a mesajului scris, din texte literare și nonliterare, în scopuri diverse, de exprimare scrisă și de utilizare corectă și adecvată a limbii române în producerea de mesaje scrise, în diferite contexte de realizare, cu scopuri diverse. Deoarece competențele de evaluat sunt ansambluri de cunoștințe, deprinderi și atitudini formate în clasele a V-a - a VIII-a, subiectele pentru evaluarea națională vor evalua atât competențele specifice și conținuturile asociate acestora, conform programei școlare actualizate pentru clasa a VIII-a (aprobată prin ordinul ministrului educației, cercetării și inovării cu nr. 5097/ din 09.09.2009), cât și conținuturile din programele școlare actualizate pentru clasele a V-a - a VII-a.
Prin evaluarea națională la limba și literatura română, în evaluarea unităților de conținut care privesc domeniul limba română (Elemente de construcție a comunicării), se are în vedere viziunea comunicativ-pragmatică, abordarea funcțională și aplicativă a elementelor de construcție a comunicării, cu accent pe identificarea rolului acestora în construirea mesajelor și pe utilizarea lor corectă și adecvată în propria exprimare scrisă. Sarcinile de lucru vizează exerciții de tip analitic (de recunoaștere, de grupare, de motivare, de descriere, de diferențiere) și de tip sintetic (de modificare, de completare, de exemplificare, de construcție), de subliniere a valorilor stilistice și de evidențiere a aspectelor ortografice și de punctuație, în situațiile care impun o asemenea abordare.
În evaluarea unităților de conținut ale domeniului lectură, sarcinile de lucru implică cerințe care privesc înțelegerea unui text dat, literar sau nonliterar (identificarea ideilor principale, a unor trăsături generale și particulare ale textului și exprimarea unui punct de vedere asupra acestora etc.), precum și redactarea de către elev a unor compuneri vizând scrierea despre un text literar sau nonliterar (rezumat, caracterizare de personaj, comentarea sumară a unor secvențe, identificarea ideilor principale, exprimarea unui punct de vedere privind ideile sau structurarea textului etc.). De asemenea, sarcinile de lucru vor avea în vedere evaluarea competențelor de redactare a unor texte argumentative (exprimarea argumentată a unui punct de vedere privind textul studiat sau la prima vedere, motivarea apartenenței la un gen literar sau la o specie literară), reflexive și imaginative (compuneri care presupun exprimarea propriilor sentimente, evidențierea trăsăturilor unui obiect într-o descriere, scurte narațiuni, continuarea logică a unor dialoguri etc.)
Pentru competențele de receptare și de producere a mesajelor orale, profesorii vor organiza activități specifice și vor realiza evaluarea de parcurs a progresului elevilor.
II. COMPETENȚE DE EVALUAT
Tabelul de mai jos cuprinde competențele generale care vizează receptarea și producerea mesajelor scrise din programa școlară pentru clasa a VIII-a (Receptarea mesajului scris, din texte literare și nonliterare, în scopuri diverse; Utilizarea corectă și adecvată a limbii române în producerea de mesaje scrise, în diferite contexte de realizare, cu scopuri diverse), detalierile lor în competențele specifice și conținuturile asociate, din programele școlare pentru clasele a V-a - a VIII-a.
1. Receptarea mesajului scris, din texte literare și nonliterare, în scopuri diverse | ||
Competențe specifice | Conținuturi asociate | |
dovedirea înțelegerii unui text literar sau nonliterar, pornind de la cerinșe date | - idei principale, idei secundare; ordinea logică și temporală a ideilor/ a întâmplărilor dintr-un text; - moduri de expunere (narațiune, descriere, dialog); - structuri în textele epice (logica acțiunii, timp, spațiu, modalități de caracterizare a personajelor, relațiile dintre personaje, naratorul) și lirice (concordanța dintre forma grafică a poeziei și ideea transmisă de aceasta, eul liric); - subiectul operei literare, momentele subiectului; - procedee de expresivitate artistică în textele studiate (figuri de stil: personificarea, alegoria, repetiția fonetică/ aliterația, metafora, hiperbola, epitetul, comparația, repetiția, enumerația, antiteză); - sensul propriu și sensul figurat al unor cuvinte într-un context dat; - elemente de versificație (măsura, rima, piciorul metric, ritmul, versul, strofa); - trăsăturile specifice genului epic, liric și dramatic în opere literare studiate sau în texte la prima vedere; - trăsături ale speciilor literare: schița, basmul popular, pastelul, fabula, nuvela, romanul, doina populară, balada populară; - texte literare (populare și culte - aparținând diverselor genuri și specii); texte nonliterare; | |
1.2 | sesizarea corectitudinii și a valorii expresive a categoriilor morfosintactice, a mijloacelor de îmbogățire a vocabularului și a categoriilor semantice studiate, a ortografiei și punctuației | - arhaisme, regionalisme și neologisme; cuvinte derivate, compuse sau obținute prin schimbarea valorii gramaticale/conversiune; - categorii semantice studiate: sinonime, antonime, omonime, cuvinte polisemantice; construcții pleonastice; sensurile cuvintelor în contexte diferite; - mijloacele interne de îmbogățire a vocabularului (derivarea, compunerea, schimbarea valorii gramaticale/conversiunea), familia de cuvinte; mijloacele externe de îmbogățire a vocabularului; - ortografierea diftongilor, a triftongilor și a vocalelor în hiat; - despărțirea cuvintelor în silabe; - semne de punctuație: punctul, virgula, două puncte, ghilimelele, linia de dialog, semnul întrebării, semnul exclamării, cratima, punctul și virgula, linia de pauză; - semne ortografice: cratima, punctul; - valori expresive ale nivelurilor limbii (fonetic, lexical și morfosintactic) într-un text dat; elemente de limbă și de stil în textul literar; figurile de stil, versificația; - categorii morfologice specifice părților de vorbire (conform programelor școlare pentru clasele a V-a - a VIII-a): părțile de vorbire flexibile (verbul, substantivul, articolul, pronumele, numeralul, adjectivul) și neflexibile (adverbul, prepoziția, conjuncția, interjecția); relații și funcții sintactice; - elemente de sintaxă a propoziției și a frazei (probleme de acord; funcții sintactice; tipuri de propoziții principale și subordonatele indicate de programa școlară; propoziția regentă, elementul regent, cuvintele și construcțiile incidente; relații sintactice; topică și punctuație; valori stilistice ale folosirii acestora în textul dat); |
1.3 | identificarea valorilor etice și culturale într-un text, cu exprimarea impresiilor și preferințelor | - elemente etice și culturale în texte literare și nonliterare și exprimarea propriei atitudini față de acestea; |
2. Utilizarea corectă și adecvată a limbii române în producerea de mesaje scrise, în diferite contexte de realizare, cu scopuri diverse | |||
Competențe specifice | Conținuturi asociate | ||
2.1 | redactarea diverselor texte, cu scopuri și destinații diverse, adaptându-le la situația de comunicare concretă | - elemente de redactare a unor compuneri pe o anumită temă/urmărind un plan dat sau conceput de elev; părțile componente ale unei compuneri; organizarea planului unei compuneri pe o temă dată; structurarea detaliilor în jurul ideii principale; dispunerea în pagină a diverselor texte; scrierea îngrijită, lizibilă și corectă; - redactarea unor texte reflexive și imaginative (compuneri care presupun exprimarea propriilor sentimente cu ocazia unui eveniment personal, social sau cultural; evidențierea unor trăsături ale unui obiect (peisaj, operă de artă, persoană)- într-o descriere; - redactarea unor scurte narațiuni; continuarea unor dialoguri; redactarea unor texte argumentative (susținerea preferințelor și a opiniilor); redactarea unor compuneri având ca suport texte literare studiate sau la prima vedere - rezumat, caracterizare de personaj; - motivarea apartenenței unui text studiat sau la prima vedere la o specie literară sau la un gen literar; - prezentarea unui punct de vedere asupra unor secvențe din texte la prima vedere, pe baza unor cerințe date (de exemplu: elemente de structură a operei literare, figurile de stil studiate, elemente de versificație etc.) sau prin exprimarea argumentată a opiniei personale privind structura textului, semnificația titlului, procedeele de expresivitate artistică învățate și semnificația/mesajul textului dat; - exprimarea argumentată a unui punct de vedere privind un text studiat sau textul la prima vedere; aprecieri personale referitoare la fragmente din textele studiate sau la prima vedere; | |
2.2 | utilizarea în redactarea unui text propriu a cunoștințelor de lexic și de morfosintaxă, folosind adecvat semnele ortografice și de punctuație | - elemente de lexic studiate în clasele V - VIII; - aplicarea corectă a cunoștințelor de morfosintaxă în exprimarea scrisă; - folosirea corectă a semnelor de punctuație la nivelul propoziției și al frazei (coordonare, subordonare, incidență); - enunțul, fraza, părți de propoziție și propoziții studiate (predicatul și propoziția subordonată predicativă, subiectul și propoziția subordonată subiectivă; atributul și propoziția subordonată atributivă; complementul direct și propoziția subordonată completivă directă; complementul indirect și propoziția subordonată completivă indirectă; complementele circumstanțiale și propozițiile subordonate circumstanțiale corespunzătoare (de loc, de timp, de mod, de cauză, de scop); propoziția subordonată circumstanțială condițională, concesivă, consecutivă; expansiunea și contragerea. | |

PROGRAMA
PENTRU DISCIPLINA
MATEMATICĂ
EVALUARE NAȚIONALĂ 2015
PROGRAMA DE EXAMEN PENTRU DISCIPLINA MATEMATICĂ
Evaluarea Națională pentru absolvenții clasei a VIII-a este un examen național și reprezintă modalitatea de evaluare externă sumativă a competențelor dobândite pe parcursul învățământului gimnazial.
În cadrul Evaluării Naționale pentru absolvenții clasei a VIII-a Matematica are statut de disciplină obligatorie.
Programa de examen este realizată în conformitate cu prevederile programei școlare în vigoare. Subiectele pentru Evaluarea Națională pentru absolvenții clasei a VIII-a evaluează competențele formate/dezvoltate pe parcursul învățământului gimnazial și se elaborează în baza prezentei programe.
COMPETENȚE GENERALE ALE DISCIPLINEI
1. Identificarea unor date și relații matematice și corelarea lor în funcție de contextul în care au fost definite
2. Prelucrarea datelor de tip cantitativ, calitativ, structural, contextual cuprinse în enunțuri matematice
3. Utilizarea algoritmilor și a conceptelor matematice pentru caracterizarea locală sau globală a unei situații concrete
4. Exprimarea caracteristicilor matematice cantitative sau calitative ale unei situații concrete și a algoritmilor de prelucrare a acestora
5. Analizarea și interpretarea caracteristicilor matematice ale unei situații-problemă
6. Modelarea matematică a unor contexte problematice variate, prin integrarea cunoștințelor din diferite domenii
COMPETENȚE DE EVALUAT ȘI CONȚINUTURI
CLASA a V-a
Competențe specifice | Conținuturi |
1. Identificarea caracteristicilor numerelor naturale și a formei de scriere a unui număr natural în contexte variate 2 Utilizarea operațiilor aritmetice și a proprietăților acestora în calcule cu numere naturale 3. Selectarea și utilizarea de algoritmi pentru efectuarea operațiilor cu numere naturale și pentru divizibilitatea cu 10,2 și 5 4 Exprimarea, în rezolvarea sau compunerea unor probleme, a soluțiilor unor ecuații de tipul: x±a=b; a±x=b; x∙a=b (a ≠ 0, a divizor al lui b); x:a=b (a ≠ 0); a:x=b (x ≠ 0, b divizor al lui a) și a unor inecuații de tipul x±a≤b (≥, <, >) x·a≤b (≥, <, >), unde a este divizor al lui b; x:a≤b (≥, <, >), cu a≠0, unde a și b sunt numere naturale 5. Deducerea unor proprietăți ale operațiilor cu numere naturale pentru a estima sau pentru a verifica validitatea unor calcule 6. Transpunerea unei situații-problemă în limbaj matematic, rezolvarea problemei obținute (utilizând ecuații, inecuații, organizarea datelor) și interpretarea rezultatului | Numere naturale • Scrierea și citirea numerelor naturale în sistemul de numerație zecimal; șirul numerelor naturale. • Reprezentarea numerelor naturale pe axa numerelor. Compararea, aproximarea și ordonarea numerelor naturale; probleme de estimare • Adunarea numerelor naturale; proprietăți. Scăderea numerelor naturale • Înmulțirea numerelor naturale; proprietăți. Factor comun. Ordinea efectuării operațiilor; utilizarea parantezelor • Ridicarea la putere cu exponent natural a unui număr natural; compararea puterilor care au aceeași bază sau același exponent • Împărțirea, cu rest zero, a numerelor naturale când împărțitorul are mai mult de o cifră • Împărțirea cu rest a numerelor naturale • Ordinea efectuării operațiilor • Noțiunea de divizor; noțiunea de multiplu. Divizibilitatea cu 10, 2, 5 • Media aritmetică a două numere naturale, cu rezultat număr natural • Ecuații și inecuații în mulțimea numerelor naturale • Probleme care se rezolvă cu ajutorul ecuațiilor și al inecuațiilor și probleme de organizare a datelor |
1. Identificarea în limbajul cotidian sau în enunțuri matematice a unor noțiuni specific teoriei mulțimilor 2. Evidențierea, prin exemple, a relațiilor de apartenență sau de incluziune 3. Selectarea și utilizarea unor modalități adecvate de reprezentare a mulțimilor și a operațiilor cu mulțimi 4. Exprimarea în limbaj matematic a unor situații concrete ce se pot descrie utilizând mulțimile 5. Interpretarea unor contexte uzuale și/sau matematice utilizând limbajul mulțimilor 6. Transpunerea unei situații-problemă în limbaj matematic utilizând mulțimi, relații și operații cu mulțimi | Mulțimi • Mulțimi: descriere și notații; element, relația dintre element și mulțime (relația de apartenență) • Relația între două mulțimi (relația de incluziune); submulțime • Mulțimile ℕ și ℕ* • Operații cu mulțimi: intersecție, reuniune, diferență • Exemple de mulțimi finite; exemple de mulțimi infinite |
1. Identificarea în limbajul cotidian sau în probleme a fracțiilor ordinare și a fracțiilor zecimale 2. Reprezentarea pe axa numerelor a fracțiilor ordinare și a fracțiilor zecimale 3. Alegerea formei de reprezentare a unui număr rațional pozitiv și utilizarea de algoritmi pentru optimizarea calculului cu fracții zecimale 4. Exprimarea, în rezolvarea sau compunerea unor probleme, a soluțiilor unor ecuații de tipul: x±a=b; a±x=b; x·a=b; (a≠0); x:a=b (a ≠ 0); a:x=b (x≠0) și a unor inecuații de tipul x±a≤b (≥,<,>), x·a≤b (≥,<,>); x:a≤b (≥,<,>) 5. Interpretarea matematică a unor probleme practice prin utilizarea operațiilor cu fracții zecimale și a ordinii efectuării operațiilor 6. Transpunerea unei situații-problemă în limbaj matematic, rezolvarea problemei obținute (utilizând ecuații sau inecuații) și interpretarea rezultatului | Numere raționale mai mari sau egale cu 0, ℚ+ Fracții ordinare • Fracții echiunitare, subunitare, supraunitare • Aflarea unei fracții dintr-un număr natural; procent • Fracții echivalente. Amplificarea și simplificarea fracțiilor • Adunarea și scăderea unor fracții ordinare care au același numitor • Reprezentarea pe axa numerelor a unei fracții ordinare Fracții zecimale • Scrierea fracțiilor ordinare cu numitori puteri ale lui 10, sub forma de fracții zecimale. • Transformarea unei fracții zecimale, cu un număr finit de zecimale nenule, într-o fracție ordinară • Aproximări la ordinul zecimilor/sutimilor. Compararea, ordonarea și reprezentarea pe axa numerelor a fracțiilor zecimale • Adunarea și scăderea fracțiilor zecimale care au un număr finit de zecimale nenule • Înmulțirea fracțiilor zecimale care au un număr finit de zecimale nenule • Ridicarea la putere cu exponent natural a unei fracții zecimale care are un număr finit de zecimale nenule • Ordinea efectuării operațiilor cu fracții zecimale finite • Împărțirea a două numere naturale cu rezultat fracție zecimală. • Transformarea unei fracții ordinare într-o fracție zecimală. Periodicitate • Împărțirea unei fracții zecimale finite la un număr natural nenul. • Împărțirea unui număr natural la o fracție zecimală finită. • Împărțirea a două fracții zecimale finite • Transformarea unei fracții zecimale într-o fracție ordinară • Ordinea efectuării operațiilor • Media aritmetică a două fracții zecimale finite • Ecuații și inecuații; probleme care se rezolvăcu ajutorul ecuațiilor |
1. Identificarea unor elemente de geometrie și a unor unități de măsură în diferite contexte 2. Caracterizarea prin descriere și desen a unei configurații geometrice date 3. Determinarea perimetrelor, a ariilor (pătrat, dreptunghi) și a volumelor (cub, paralelipiped dreptunghic) și exprimarea acestora în unități de măsură corespunzătoare 4. Transpunerea în limbaj specific geometriei a unor probleme practice referitoare la perimetre, arii, volume, utilizând transformarea convenabilă a unităților de măsură 5. Interpretarea unei configurații geometrice în sensul recunoașterii elementelor ei și a relaționării cu unitățile de măsură studiate 6. Analizarea și interpretarea rezultatelor obținute prin rezolvarea unor probleme practice cu referire la figurile geometrice și la unitățile de măsură studiate | Elemente de geometrie și unități de măsură • Dreapta, segmentul de dreaptă, măsurarea unui segment de dreaptă • Unghiul, triunghiul, patrulaterul, cercul: prezentare prin descriere și desen; recunoașterea elementelor lor: laturi, unghiuri, diagonale, centrul și raza cercului • Simetria, axa de simetrie și translația: prezentare intuitivă, exemplificare în triunghi, cerc, patrulater • Cubul, paralelipipedul dreptunghic: prezentare prin desen și desfășurare; recunoașterea elementelor lor: vârfuri, muchii, fețe • Unități de măsură pentru lungime; perimetre;transformări • Unități de măsură pentru arie; aria pătratului și a dreptunghiului; transformări • Unități de măsură pentru volum; volumul cubului și al paralelipipedului dreptunghic; transformări • Unități de măsură pentru capacitate; transformări • Unități de măsură pentru masă; transformări • Unități de măsură pentru timp; transformări • Unități monetare; transformări |
CLASA a VI-a
Competențe specific | Conținuturi |
1 Identificarea în exemple, în exerciții sau în probleme a noțiunilor: divizor, multiplu, numere prime, numere compuse, c.m.m.d.c, c.m.m.m.c 2. Aplicarea criteriilor de divizibilitate (cu 10, 2, 5, 3, 9) pentru descompunerea numerelor naturale în produs de puteri de numere prime 3. 3. Utilizarea algoritmilor pentru determinarea c.m.m.d.c, c.m.m.m.c a două sau a mai multor numere naturale 4. 4. Exprimarea unor caracteristici ale relației de divizibilitate în mulțimea numerelor naturale, în exerciții și probleme care se rezolvă folosind divizibilitatea 5. 5. Deducerea unor reguli de calcul cu puteri și a unor proprietăți ale divizibilității în mulțimea numerelor naturale, în exerciții și probleme 6. 6. Transpunerea unei situații-problemă în limbajul divizibilității în mulțimea numerelor naturale, rezolvarea problemei obținute și interpretarea rezultatului | ALGEBRĂ Mulțimea numerelor naturale • Operații cu numere naturale; reguli de calcul cu puteri • • Divizor, multiplu. Criteriile de divizibilitate cu 10, 2, 5, 3, 9 • • Numere prime și numere compuse • Descompunerea numerelor naturale în produs de puteri de numere prime • Proprietăți ale relației de divizibilitate în ℕ : a|a , pentru orice a ∊ ℕ; a|b și b|a ⇒ a=b, pentru orice a,b∊ℕ a|b și b|c ⇒ a|c, pentru orice a,b,c ∊ ℕ a|b ⇒ a|k·b, pentru orice a,b,k ∊ ℕ a|b și a|c ⇒ a|(b ± c), pentru orice a,b,c ∊ ℕ • Divizori comuni a două sau mai multor numere naturale; c.m.m.d.c.; numere prime între ele • • Multipli comuni a două sau mai multor numere naturale; c.m.m.m.c.; relația dintre c.m.m.d.c. și c.m.m.m.c. • Probleme simple care se rezolvă folosind divizibilitatea |
1 Recunoașterea fracțiilor echivalente, a fracțiilor ireductibile și a formelor de scriere a unui număr rațional 2. 2. Aplicarea regulilor de calcul cu numere raționale pozitive pentru rezolvarea ecuațiilor de tipul: x±a=b, x·a=b, x:a=b (a≠0), ax±b=c, unde a,b,c, sunt numere raționale pozitive 3. 3. Utilizarea proprietăților operațiilor în efectuarea calculelor cu numere raționale pozitive 4. 4. Redactarea soluțiilor unor probleme rezolvate prin ecuațiile studiate în mulțimea numerelor raționale pozitive 5. 5. Determinarea regulilor de calcul eficiente în efectuarea calculelor cu numere raționale pozitive 6. 6. Interpretarea matematică a unor probleme practice prin utilizarea operațiilor cu numere raționale pozitive și a ordinii efectuării operațiilor | Mulțimea numerelor raționale pozitive • Fracții echivalente; fracție ireductibilă; noțiunea de număr rațional; forme de scriere a unui număr rațional; ℕ ⊂ ℚ • • Adunarea numerelor raționale pozitive; scăderea numerelor rationale pozitive • Înmulțirea numerelor raționale pozitive • • Ridicarea la putere cu exponent natural a unui număr rațional pozitiv; reguli de calcul cu puteri • Împărțirea numerelor raționale pozitive • Ordinea efectuării operațiilor cu numere raționale pozitive • Media aritmetică ponderată a unor numere raționale pozitive • • Ecuații în mulțimea numerelor raționale pozitive • • Probleme care se rezolvă cu ajutorul ecuațiilor |
1. 1. Identificarea rapoartelor, proporțiilor și a mărimilor direct sau invers proporționate în enunțuri diverse 2. 2. Reprezentarea unor date sub formă de tabele sau de diagrame statistice în vederea înregistrării, prelucrării și prezentării acestora 3. 3. Alegerea metodei adecvate de rezolvare a problemelor în care intervin rapoarte, proporții și mărimi direct sau invers proporționate 4. 4. Caracterizarea și descrierea mărimilor care apar în rezolvarea unor probleme prin regula de trei simplă 5. 5. Analizarea unor situații practice cu ajutorul rapoartelor, procentelor sau proporțiilor 6. 6. Rezolvarea cu ajutorul rapoartelor și proporțiilor a unor situații-problemă și interpretarea rezultatelor | Rapoarte și proporții • Rapoarte; procente; probleme în care intervin procente • Proporții; proprietatea fundamentală a proporțiilor, aflarea unui termen necunoscut dintr-o proporție • • Proporții derivate • Mărimi direct proporționale; regula de trei simplă • Mărimi invers proporționale; regula de trei simplă • Elemente de organizare a datelor; reprezentarea datelor prin grafice; probabilități |
1. 1. Identificarea caracteristicilor numerelor întregi în contexte variate 2. 2. Utilizarea operațiilor cu numere întregi și a proprietăților acestora în rezolvarea ecuațiilor și a inecuațiilor 3. 3. Aplicarea regulilor de calcul și folosirea parantezelor în efectuarea operațiilor cu numere întregi 4. 4. Redactarea soluțiilor ecuațiilor și inecuațiilor studiate în mulțimea numerelor întregi, în rezolvarea sau în compunerea unei probleme 5. 5. Interpretarea unor date din probleme care se rezolvă utilizând numerele întregi 6. 6. Transpunerea unei situații-problemă în limbaj algebric, rezolvarea problemei obținute și interpretarea rezultatului | Numere întregi • Mulțimea numerelor întregi ℤ; opusul unui număr întreg; reprezentarea pe axa numerelor; valoare absolută (modulul); compararea și ordonarea numerelor întregi • • Adunarea numerelor întregi; proprietăți • Scăderea numerelor întregi • Înmulțirea numerelor întregi; proprietăți; mulțimea multiplilor unui număr întreg • Împărțirea numerelor întregi când deîmpărțitul este multiplu al împărțitorului; mulțimea divizorilor unui număr întreg • • Puterea unui număr întreg cu exponent număr natural; reguli de calcul cu puteri • • Ordinea efectuării operațiilor și folosirea parantezelor • • Ecuații în ℤ; inecuații în ℤ • • Probleme care se rezolvă cu ajutorul ecuațiilor |
1. 1. Recunoașterea și descrierea unor figuri geometrice plane în configurații date 2. 2. Stabilirea coliniarității unor puncte și verificarea faptului că două unghiuri sunt adiacente, complementare sau suplementare 3. 3. Utilizarea proprietăților referitoare la drepte și unghiuri pentru calcularea unor lungimi de segmente și a măsurilor unor unghiuri 4. 4. Exprimarea prin reprezentări geometrice a noțiunilor legate de drepte și unghiuri 5. 5. Alegerea reprezentărilor geometrice adecvate în vederea optimizării calculelor de lungimi de segmente și de măsuri de unghiuri 6. 6. Interpretarea informațiilor conținute în reprezentări geometrice în corelație cu determinarea unor lungimi de segmente și a unor măsuri de unghiuri | GEOMETRIE Dreapta • • Punct, dreaptă, plan, semiplan, semidreaptă, segment (descriere, reprezentare, notații) • Pozițiile relative ale unui punct față de o dreaptă; puncte coliniare; “prin două puncte distincte trece o dreaptă și numai una" (introducerea noțiunilor de: axiomă, teoremă directă, ipoteză concluzie, demonstrație, teoremă reciprocă) • Pozițiile relative a două drepte: drepte concurente, drepte paralele • Distanța dintre două puncte; lungimea unui segment • Segmente congruente; mijlocul unui segment; simetricul unui punct față de un punct; construcția unui segment congruent cu un segment dat Unghiuri • Definiție, notații, elemente; interiorul unui unghi, exteriorul unui unghi; unghi nul, unghi cu laturile în prelungire • Măsurarea unghiurilor cu raportorul; unghiuri congruente; unghi drept, unghi ascuțit, unghi obtuz • • Calcule cu măsuri de unghiuri exprimate în grade și minute sexagesimale. Unghiuri suplementare, unghiuri complementare • Unghiuri adiacente; bisectoarea unui unghi • Unghiuri opuse la vârf, congruența lor; unghiuri formate în jurul unui punct, suma măsurilor lor |
1. 1. Identificarea triunghiurilor în configurații geometrice date 2. 2. Stabilirea congruenței triunghiurilor oarecare 3. 3. Clasificarea triunghiurilor după anumite criterii date sau alese 4. 4. Exprimarea proprietăților figurilor geometrice în limbaj matematic 5. 5. Interpretarea cazurilor de congruență a triunghiurilor în corelație cu cazurile de construcție a triunghiurilor 6. 6. Aplicarea metodei triunghiurilor congruente în rezolvarea unor probleme matematice sau practice | Congruența triunghiurilor • Triunghi: definiție, elemente; clasificarea triunghiurilor; perimetrul triunghiului • • Construcția triunghiurilor: cazurile LUL, ULU, LLL. Congruența triunghiurilor oarecare: criterii de congruență a triunghiurilor: LUL, ULU, LLL • • Metoda triunghiurilor congruente |
1. 1. Recunoașterea și descrierea unor elemente de geometrie plană în configurații geometrice date 2. 2. Utilizarea instrumentelor geometrice (riglă, echer, raportor, compas) pentru a desena figuri geometrice plane descrise în contexte matematice date 3. 3. Determinarea și aplicarea criteriilor de congruență ale triunghiurilor dreptunghice 4. 4. Exprimarea poziției dreptelor în plan (paralelism, perpendicularitate) prin definiții, notații, desen 5. 5. Intrepretarea perpendicularității în relație cu paralelismul și cu distanța dintre două puncte 6. Transpunerea unei situații-problemă în limbaj geometric, rezolvarea problemei obținute și interpretarea rezultatului | Perpendicularitate • • Drepte perpendiculare (definiție, notație, construcție cu echerul); oblice; distanța de la un punct la o dreaptă. Înălțimea în triunghi (definiție, desen). Concurența înălțimilor într-un triunghi (fără demonstrație) • Criteriile de congruență ale triunghiurilor dreptunghice: IC, IU, CC, CU • Aria triunghiului (intuitiv pe rețele de pătrate) • Mediatoarea unui segment; proprietatea punctelor de pe mediatoarea unui segment; construcția mediatoarei unui segment cu rigla și compasul; concurența mediatoarelor laturilor unui triunghi; simetria față de o dreaptă • • Proprietatea punctelor de pe bisectoarea unui unghi; construcția bisectoarei unui unghi cu rigla și compasul; concurența bisectoarelor unghiurilor unui triunghi Paralelism • Drepte paralele (definiție, notație); construirea dreptelor paralele (prin translație); axioma paralelelor • Criterii de paralelism (unghiuri formate de două drepte paralele cu o secantă) |
1. 1. Recunoașterea și descrierea unor proprietăți ale triunghiurilor în configurații geometrice date 2. 2. Calcularea unor lungimi de segmente și a unor măsuri de unghiuri utilizând metode adecvate 3. Utilizarea unor concepte matematice în triunghiul isoscel, în triunghiul echilateral sau în triunghiul dreptunghic 4. 4. Exprimarea caracteristicilor matematice ale triunghiurilor și ale liniilor importante în triunghi prin definiții, notații și desen 5. 5. Deducerea unor proprietăți ale triunghiurilor folosind noțiunile studiate 6. 6. Interpretarea informațiilor conținute în probleme legate de proprietăți ale triunghiurilor | Proprietăți ale triunghiurilor • Suma măsurilor unghiurilor unui triunghi; unghi exterior unui triunghi, teorema unghiului exterior • Mediana în triunghi; concurența medianelor unui triunghi (fără demonstrație) • Proprietăți ale triunghiului isoscel (unghiuri, linii importante, simetrie) • Proprietăți ale triunghiului echilateral (unghiuri, linii importante, simetrie) • Proprietăți ale triunghiului dreptunghic (cateta opusă unghiului de 30˚ , mediana corespunzătoare ipotenuzei - teoreme directe și reciproce) |
CLASA a VII-a
Competențe specific | Conținuturi |
1. Identificarea caracteristicilor numerelor raționale și a formelor de scriere a acestora în contexte variate 2. Aplicarea regulilor de calcul cu numere raționale, a estimărilor și a aproximărilor pentru rezolvarea unor ecuații 3. Utilizarea proprietăților operațiilor în efectuarea calculelor cu numere raționale 4. Caracterizarea mulțimilor de numere și a relațiilor dintre acestea utilizând limbajul logicii matematice și teoria mulțimilor 5. Determinarea regulilor eficiente de calcul în efectuarea operațiilor cu numere raționale 6. Interpretarea matematică a unor probleme practice prin utilizarea operațiilor cu numere raționale și a ordinii efectuării operațiilor | ALGEBRĂ Mulțimea numerelor raționale • Mulțimea numerelor raționale ℚ; reprezentarea numerelor raționale pe axa numerelor, opusul unui număr rațional; valoarea absolută (modulul); ℕ ⊂ ℤ ⊂ ℚ • Operații cu numere raționale, proprietăți • Compararea și ordonarea numerelor raționale • Ordinea efectuării operațiilor și folosirea parantezelor • Ecuația de forma ax+b=0, cu a∊ℚ*, b∊ℚ • Probleme care se rezolvă cu ajutorul ecuațiilor |
1. Identificarea caracteristicilor numerelor reale și a formelor de scriere a acestora în contexte variate 2. Aplicarea regulilor de calcul cu numere reale, a estimărilor și a aproximărilor pentru rezolvarea unor ecuații 3. Utilizarea proprietăților operațiilor în efectuarea calculelor cu numere reale 4. Caracterizarea mulțimilor de numere și a relațiilor dintre acestea utilizând limbajul logicii matematice și teoria mulțimilor 5. Determinarea regulilor de calcul eficiente în efectuarea operațiilor cu numere reale 6. Interpretarea matematică a unor probleme practice prin utilizarea operațiilor cu numere reale și a ordinii efectuării operațiilor | Mulțimea numerelor reale • Rădăcina pătrată a unui număr natural pătrat perfect • Algoritmul de extragere a rădăcinii pătrate dintr-un număr natural; aproximări • Exemple de numere iraționale; mulțimea numerelor reale, ℝ modulul unui număr real: definiție, proprietăți; compararea și ordonarea numerelor reale; reprezentarea numerelor reale pe axa numerelor prin aproximări; ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ • Reguli de calcul cu radicali: scoaterea factorilor de sub radical, introducerea factorilor sub radical,
• Operații cu numere reale (adunare, scădere, înmulțire, împărțire, ridicare la putere, raționalizarea numitorului de formă • Media aritmetică a n numere reale, n≥2; media geometrică a două numere reale pozitive |
1. Identificarea unor reguli de calcul numeric sau algebric pentru simplificarea unor calcule 2. Utilizarea operațiilor cu numere reale și a proprietăților acestora în rezolvarea unor ecuații și a unor inecuații 3. Aplicarea regulilor de calcul și folosirea parantezelor în efectuarea operațiilor cu numere reale 4. Redactarea rezolvării ecuațiilor și a inecuațiilor studiate în mulțimea numerelor reale 5. Obținerea unor inegalități echivalente prin operare în ambii membri: 1) a≤a, pentru orice a ∊ ℝ; 2) a≤b și b≤a ⇒ a=b, pentru orice a, b ∊ ℝ 3) a≤b și b≤c ⇒ a≤c, pentru orice a,b,c ∊ ℝ 4) a≤b și c ∊ ℝ⇒ a±c≤b±c, pentru orice a, b ∊ ℝ 5) a≤b și c>0 ⇒ ac≤bc și a:c ≤ b:c, pentru orice a, b ∊ ℝ 6) a≤b și c<0 ⇒ ac ≥ bc și a:c ≥ b:c, pentru orice a,b ∊ ℝ 6. Transpunerea unei situații-problemă în limbajul ecuațiilor și/sau al inecuațiilor, rezolvarea problemei obținute și interpretarea rezultatului | Calcul algebric • Calcule cu numere reale reprezentate prin litere: adunare/scadere, înmulțire, împărțire, ridicare la putere, reducerea termenilor asemenea • Formule de calcul prescurtat: (a+b)2=a2±2ab+b2; (a-b)(a+b)=a2-b2, unde a,b∊ℝ • Descompuneri în factori utilizând reguli de calcul în ℝ • Ecuația de forma x2=a, unde a∊ℚ+ Ecuații și inecuații • Proprietăți ale relației de egalitate în mulțimea numerelor reale • Ecuații de formă ax+b=0, unde a,b∊ ℝ; mulțimea soluțiilor unei ecuații; ecuații echivalente • Proprietăți ale relației de inegalitate "≤" pe mulțimea numerelor reale • Inecuații de forma ax+b>0 (<,≤,≥), cu a,b ∊ ℝ și x∊ℤ • Probleme care se rezolvă cu ajutorul ecuațiilor și inecuațiilor |
1. Identificarea unor corespondențe între diferite reprezentări ale acelorași date 2. Reprezentarea unor date sub formă de grafice, tabele sau diagrame statistice în vederea înregistrării, prelucrării și prezentării acestora 3. Alegerea metodei adecvate de rezolvare a problemelor în care intervin dependențe funcționale sau calculul probabilităților 4. Caracterizarea și descrierea unor elemente geometrice într-un sistem de axe ortogonale 5. Analizarea unor situații practice cu ajutorul elementelor de organizare a datelor 6. Transpunerea unei relații dintr-o formă în alta (text, formulă, diagramă, grafic) | Elemente de organizare a datelor • Produsul cartezian a două mulțimi nevide. Reprezentarea într-un sistem de axe perpendiculare (ortogonale) a unor perechi de numere întregi • Reprezentarea punctelor în plan cu ajutorul sistemului de axe ortogonale; distanța dintre două puncte din plan • Reprezentarea și interpretarea unor dependențe funcționale prin tabele, diagrame și grafice • Probabilitatea realizării unor evenimente |
1. Recunoașterea și descrierea patrulaterelor în configurații geometrice date 2. Identificarea patrulaterelor particulare utilizând proprietăți precizate 3. Utilizarea proprietăților calitative și metrice ale patrulaterelor în rezolvarea unor probleme 4. Exprimarea prin reprezentări geometrice a noțiunilor legate de patrulatere 5. Alegerea reprezentărilor geometrice adecvate în vederea optimizării calculelor de lungimi de segmente, de măsuri de unghiuri și de arii 6. Interpretarea informațiilor deduse din reprezentări geometrice în corelație cu anumite situații practice | GEOMETRIE Patrulatere • Patrulater convex (definiție, desen) • Suma măsurilor unghiurilor unui patrulater convex • Paralelogram; proprietăți • Paralelograme particulare: dreptunghi, romb și pătrat; proprietăți • Trapez, clasificare; trapez isoscel, proprietăți • Arii (triunghiuri, patrulatere) |
1. Identificarea perechilor de triunghiuri asemenea în configurații geometrice date 2. Stabilirea relației de asemănare între două triunghiuri prin metode diferite 3. Utilizarea noțiunii de paralelism pentru caracterizarea locală a unei configurații geometrice date 4. Exprimarea proprietăților figurilor geometrice (segmente, triunghiuri, patrulatere) în limbaj matematic 5. Interpretarea asemănării triunghiurilor în corelație cu proprietăți calitative și/ sau metrice 6. Aplicarea asemănării triunghiurilor în rezolvarea unor probleme matematice sau practice | Asemănarea triunghiurilor • Segmente proporționate • Teorema paralelelor echidistante. Împărțirea unui segment în părți proporționale cu numere (segmente) date. Teorema lui Thales (fără demonstrație). Teorema reciprocă a teoremei lui Thales • Linia mijlocie în triunghi; proprietăți. Centrul de greutate al unui triunghi • Linia mijlocie în trapez; proprietăți • Triunghiuri asemenea • Criterii de asemănare a triunghiurilor • Teorema fundamentală a asemanării |
1. Recunoașterea și descrierea elementelor unui triunghi dreptunghic într-o configurație geometrică dată 2. Aplicarea relațiilor metrice într-un triunghi dreptunghic pentru determinarea unor elemente ale acestuia 3. Deducerea relațiilor metrice într-un triunghi dreptunghic 4. Exprimarea, în limbaj matematic, a perpendicularității a două drepte prin relații metrice 5. Interpretarea perpendicularității în relație cu rezolvarea triunghiului dreptunghic 6. Transpunerea rezultatelor obținute prin rezolvarea unor triunghiuri dreptunghice la situații-problemă date | Relații metrice în triunghiul dreptunghic • Proiecții ortogonale pe o dreaptă • Teorema înălțimii • Teorema catetei • Teorema lui Pitagora; teorema reciprocă a teoremei lui Pitagora • Noțiuni de trigonometrie în triunghiul dreptunghic: sinusul, cosinusul, tangenta și cotangenta unui unghi ascuțit • Rezolvarea triunghiului dreptunghic |
1. Recunoașterea și descrierea elementelor unui cerc, într-o configurație geometrică dată 2. Calcularea unor lungimi de segmente și a unor măsuri de unghiuri utilizând metode adecvate în configurații geometrice care conțin un cerc 3. Utilizarea informațiilor oferite de o configurație geometrică pentru deducerea unor proprietăți ale cercului 4. Exprimarea proprietăților elementelor unui cerc în limbaj matematic 5. Deducerea unor proprietăți ale cercului și ale poligoanelor regulate folosind reprezentări geometrice și noțiuni studiate 6. Interpretarea informațiilor conținute în probleme practice legate de cerc și de poligoane regulate | Cercul • Cercul: definiție; elemente în cerc: centru, rază, coardă, diametru, arc; interior, exterior; discul • Unghi la centru; măsura arcelor; arce congruente • Coarde și arce în cerc (la arce congruente corespund coarde congruente, și reciproc; proprietatea diametrului perpendicular pe o coardă; proprietatea arcelor cuprinse între coarde paralele; proprietatea coardelor egal depărtate de centru) • Unghi înscris în cerc; triunghi înscris în cerc • Pozițiile relative ale unei drepte față de un cerc; tangente dintr-un punct exterior la un cerc; triunghi circumscris unui cerc • Poligoane regulate: definite, desen • Calculul elementelor (latură, apotemă, arie, perimetru) în următoarele poligoane regulate: triunghi echilateral, pătrat, hexagon regulat • Lungimea cercului și aria discului |
CLASA a VIII-a
Competențe specific | Conținuturi |
1. Identificarea în exemple, în exerciții sau în probleme a numerelor reale și a formulelor de calcul prescurtat 2. Utilizarea în exerciții a definiției intervalelor de numere reale și reprezentarea acestora pe axa numerelor 3. Alegerea formei de reprezentare a unui număr real și utilizarea de algoritmi pentru optimizarea calculului cu numere reale 4. Folosirea terminologiei aferente noțiunii de număr real (semn, modul, opus, invers, parte întreagă, parte fracționară) în contexte variate 5. Deducerea și aplicarea formulelor de calcul prescurtat pentru optimizarea unor calcule 6. Rezolvarea unor situații problemă utilizând rapoarte de numere reale reprezentate prin litere; interpretarea rezultatului | ALGEBRĂ 1. Numere reale ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ. Reprezentare numerelor reale pe axa numerelor prin aproximări. Modulul unui număr real. Intervale de numere reale • Operații cu numere reale; raționalizarea numitorului de formă • Calcule cu numere reale reprezentate prin litere; formule de calcul prescurtat: (a±b)2 = a2±2ab+b2; (a+b)(a-b)=a2-b2 (a+b+c)2=a2+b2+c2+2ab+2bc+2ac • Descompuneri în factori (factor comun, grupare de termeni, formule de calcul) • Rapoarte de numere reale reprezentate prin litere; operații cu acestea (adunare, scădere, înmulțire, împărțire, ridicare la putere) |
1. Recunoașterea unor corespondente care sunt funcții 2. Utilizarea valorilor unor funcții în rezolvarea unor ecuații și a unor inecuații 3. Reprezentarea în diverse moduri a unor corespondențe și/sau a unor funcții în scopul caracterizării acestora 4. Exprimarea prin reprezentări grafice a unor noțiuni de geometrie plană 5. Determinarea soluțiilor unor ecuații, inecuații sau sisteme de ecuații 6. Identificarea unor probleme care se rezolvă cu ajutorul ecuațiilor, inecuațiilor sau a sistemelor de ecuații, rezolvarea acestora și interpretarea rezultatului obținut | Funcții • Noțiunea de funcție • Funcții definite pe mulțimi finite exprimate cu ajutorul unor diagrame, tabele, formule; graficul unei funcții, reprezentarea geometrică a graficului • Funcții de tipul ƒ:A →ℝ, ƒ(x)=ax+b, a,b∊ℝ, unde A=ℝ sau A este o mulțime finită; reprezentarea geometrică a graficului funcției ƒ; interpretare geometrică 2. Ecuații, inecuații și sisteme de ecuații • Ecuații de forma ax+b=0,unde a și b sunt numere reale • Ecuații de forma ax+by+c=0,unde a,b,c sunt numere reale,a≠0, b≠0 • Sisteme de ecuații de forma
sunt numere reale; rezolvare prin metoda substituției și/sau prin metoda reducerii; interpretare geometrică • Ecuația de forma ax2+bx+c=0, unde a,b,c sunt numere reale, a≠0 • Inecuații de forma ax+b>0, (≥,<,≤) unde a și b sunt numere reale • Probleme care se rezolvă cu ajutorul ecuațiilor, inecuațiilor și a sistemelor de ecuații |
1. Recunoașterea și descrierea unor proprietăți ale unor figuri geometrice plane în configurații date în spațiu sau pe desfășurări ale acestora 2. Folosirea instrumentelor geometrice adecvate pentru reprezentarea, prin desen, în plan, a corpurilor geometrice 3. Utilizarea proprietăților referitoare la drepte și unghiuri în spațiu pentru analizarea pozițiilor relative ale acestora 4. Exprimarea prin reprezentări geometrice a noțiunilor legate de drepte și unghiuri în plan și în spațiu 5. Alegerea reprezentărilor geometrice adecvate în vederea optimizării descrierii configurațiilor spațiale și în vederea optimizării calculelor de lungimi de segmente și de măsuri de unghiuri 6. Interpretarea reprezentărilor geometrice și a unor informații deduse din acestea, în corelație cu determinarea unor lungimi de segmente și a unor măsuri de unghiuri | GEOMETRIE Relații între puncte, drepte și plane • Puncte, drepte, plane: convenții de desen și de notație • Determinarea dreptei; determinarea planului • Piramida: descriere și reprezentare; tetraedrul • Prisma: descriere și reprezentare; paralelipipedul dreptunghic; cubul • Poziții relative a două drepte în spațiu; relația de paralelism în spațiu • Unghiuri cu laturile respectiv paralele (fără demonstrație); unghiul a două drepte în spațiu; drepte perpendiculare • Poziții relative ale unei drepte față de un plan; dreapta perpendiculară pe un plan; distanța de la un punct la un plan (descriere și reprezentare); înălțimea piramidei (descriere și reprezentare) • Poziții relative a două plane; plane paralele; distanța dintre două plane paralele (descriere și reprezentare); înălțimea prismei (descriere și reprezentare); secțiuni paralele cu baza în corpurile geometrice studiate • Trunchiul de piramidă: descriere și reprezentare Proiecții ortogonale pe un plan • Proiecții de puncte, de segmente de dreaptă și de drepte pe un plan • Unghiul dintre o dreaptă și un plan; lungimea proiecției unui segment • Teorema celor trei perpendiculare; calculul distanței de la un punct la o dreaptă; calculul distanței de la un punct la un plan; calculul distanței dintre două plane paralele • Unghi diedru; unghi plan corespunzător diedrului; unghiul dintre două plane; plane perpendiculare • Calculul unor distanțe și măsuri de unghiuri pe fețele sau în interiorul corpurilor studiate. |
1. Identificarea unor elemente ale figurilor geometrice plane în configurații geometrice spațiale date 2. Calcularea ariilor și volumelor corpurilor geometrice studiate 3. Clasificarea corpurilor geometrice după anumite criterii date sau alese 4. Exprimarea proprietăților figurilor și corpurilor geometrice în limbaj matematic (axiomă, teoremă directă, teoremă reciprocă, ipoteză, concluzie, demonstrație) 5. Analizarea și interpretarea condițiilor necesare pentru ca o configurație geometrică să verifice anumite cerințe 6. Transpunerea unor situații-problemă în limbaj geometric, rezolvarea problemei obținute și interpretarea rezultatului | Calcularea de arii și volume • Paralelipipedul dreptunghic, cubul: descriere, desfășurare, aria laterală, aria totală și volum • Prisma dreaptă cu baza: triunghi echilateral, pătrat, dreptunghi, hexagon regulat: descriere, desfășurare, aria laterală, aria totală și volum • Piramida triunghiulară regulată, tetraedrul regulat, piramida patrulateră regulată, piramida hexagonală regulată: descriere, desfășurare, aria laterală, aria totală și volum • Trunchiul de piramidă triunghiulară regulată, trunchiul de piramidă patrulateră regulată: descriere, desfașurare, aria laterală, aria totală, volum • Cilindrul circular drept, conul circular drept, trunchiul de con circular drept: descriere, desfășurare, secțiuni paralele cu baza și secțiuni axiale; aria laterală, aria totală și volumul. • Sfera: descriere, aria, volumul |
Se recomandă, din punct de vedere didactic, abordarea conținuturilor din perspectiva formării/dezvoltării competențelor specifice care le sunt asociate de programă. Acest lucru presupune centrarea demersului didactic asupra acțiunilor care trebuie realizate pentru a forma/dezvolta la elevi competențele prevăzute de programa școlară și pentru ca aceștia să demonstreze, în cadrul evaluărilor, însușirea acestora.
| ← Ordinul MEN nr. 4430/2014 - organizarea şi desfăşurarea... | Ordinul MEN nr. 4432/2014 - organizarea şi desfăşurarea... → |
|---|